2015 CMU 15-213 CSAPP
Lab1(datalab): Manipulating bits
Lab2(bomblab): Defusing a binary bomb
Lab3(attacklab): The basics of code injection attacks
Lab4(cachelab): Build a cache simulator
Lab5(tshlab): Unix Shell
Lab6(malloclab): malloc package
Lab7(proxylab): Web proxy
Lecture 01 Bits,Bytes,and Integer
位(Bit):计算机中存储信息的最小单位。可以存储一个二进制数,表示两种状态。
字节(Byte):计算机中存储信息都基本单位。八个二进制位为一个字节。
字(Word):字是计算机处理信息的基本单位,其大小取决于计算机体系结构和操作系统。一个字由若干个字节组成,通常是2个字节、4个字节或更多。
字长(Word Length):字长指的是计算机处理器一次能处理的二进制数据的位数。它决定了计算机的运算能力和数据存储的最大范围。常见的字长包括16位、32位、64位等。也称作机器字长。
- 虚拟地址空间是由机器字长决定的。虚拟地址空间是一个进程可用于存储其代码、数据和堆栈等的抽象地址空间。在32位系统中,虚拟地址空间的最大大小通常是2^32 字节(或4GB),一个32位地址可以表示的最大地址是2^32。
32位二进制表示过于复杂,常用十六位表示
例如0x80000000指的是int的最小值T_min
1 | 0x指十六进制 |
Shift Operations
Left Shift : x<<y
左侧多余位删除。
右侧补0。
当左移的位数超过该数值类型的最大位数时,编译器会用左移的位数去模类型的最大位数,然后按余数进行移位,如:
int i = 1, j = 0x80000000; //设int为32位
i = i << 33; // 33 % 32 = 1 左移1位,i变成2;
j = j << 33; // 33 % 32 = 1 左移1位,j变成0,最高位被丢弃;在用gcc编译这段程序的时候编译器会给出一个warning,说左移位数>=类型长度.那么实际上i,j移动的就是1位(33%32)。
Right Shift : x>>y
右侧多余位删除。
Logical shift (逻辑移位) : 空缺位用0填充。有符号数的右移是逻辑右移。
Arithmetic shift(算数移位): 空缺位用符号位填充。有符号数的右移是算数右移
当移动的位数超过类型的长度时,会取余数,然后移动余数个位。
/1.png)
Numeric Ranges
| Unsigned Values | Two’s Complement Values |
|---|---|
| UMin = 0 | TMin = -2^(w-1) |
| 000…0 | 100…0 |
| UMax = 2^w-1 | TMax = 2^(w-1)-1 |
| 111…1 | 011…1 |
掩码运算
从一个字节中选出位的集合。
比如掩码0xFF表示一个字的低字节。
x&0xFF表示生成一个由x的最低有效字节组成的值,其他字节被置为0。
Casting Surprise
- 整数溢出:当一个整数值超出了其数据类型的最大值或最小值时,会发生整数溢出。在C语言中,整数溢出会导致“溢出”值被截断,从而循环回最小值或最大值。
- 有符号与无符号整数:有符号整数可以表示正数、负数和零,而无符号整数只能表示非负数(包括零)。当有符号整数与无符号整数进行操作时,有符号整数会被转换为无符号整数。
- 有符号数的补码的最高位,不仅有符号位的意思,还有权重的意思。
Exercise2-21
表达式 类型 求值 -2147483647-1 == 2147483648U 无符号 1 -2147483647-1 < 2147483647 有符号 1 -2147483647-1U < 2147483647 无符号 0 -2147483647-1 < -2147483647 有符号 1 -2147483647-1U < -2147483647 无符号 1 T_min = -2147483648
T_minU = 2147483648
-1U = 4294967295
sizeof得到的值为usigned value
原码 补码 反码
同余
两个整数a,b,若它们除以整数m所得的余数相等,则称a,b对于模m同余
记作 a ≡ b (mod m)
读作 a 与 b 关于模 m 同余。
举例说明:
4 mod 12 = 4
16 mod 12 = 4
28 mod 12 = 4
所以4, 16, 28关于模 12 同余。
负数取模
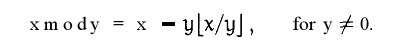
x mod y等于 x 减去 y 乘上 x与y的商的下界。
以 -3 mod 2 举例:
-3 mod 2
= -3 - 2x[-3/2 ]
= -3 - 2x[-1.5]
= -3 - 2x(-2)
= -3 + 4 = 1
(-2) mod 12 = 12-2=10
(-4) mod 12 = 12-4 = 8
(-5) mod 12 = 12 - 5 = 7
同余的定理
- 反身性 : a ≡ a (mod m)
- 线性运算定理:
如果a ≡ b (mod m),c ≡ d (mod m) 那么:
(1)a ± c ≡ b ± d (mod m)
(2)a * c ≡ b * d (mod m)
一个数的反码, 实际上是这个数对于一个模的同余数。
而2+126很显然相当于钟表转过了一轮, 而因为符号位是参与计算的, 正好和溢出的最高位形成正确的运算结果。
既然反码可以将减法变成加法, 那么现在计算机使用的补码呢? 为什么在反码的基础上加1, 还能得到正确的结果?
2-1=2+(-1) = [0000 0010]原 + [1000 0001]原 = [0000 0010]补 + [1111 1111]补
如果把[1111 1111]当成原码, 去除符号位, 则:
[0111 1111]原 = 127
其实, 在反码的基础上+1, 只是相当于增加了模的值:
(-1) mod 128 = 127
127 mod 128 = 127
2-1 ≡ 2+127 (mod 128)
此时, 表盘相当于每128个刻度转一轮. 所以用补码表示的运算结果最小值和最大值应该是[-128, 128]。
但是由于0的特殊情况, 没有办法表示128, 所以补码的取值范围是[-128, 127]。

评论区
欢迎你留下宝贵的意见,昵称输入QQ号会显示QQ头像哦~