算法与分治

Divide and Conquer（DC）

Divide：将源问题分解为规模较小的子问题，拆分问题性质相同，将子问题的解组合成原问题的解。

Conquer：如果子问题仍然困难，就继续对子问题进行分解，直到子问题可以被trivial。

Recursion：用递归的方式实现。

归并排序

问题定义：

• 输入：n个数构成的数组;

• 输出：排列该n个数的有序数组。

Merg Sort：

• 分解：将原数组等分为两个子数组;
• 求解：递归地对两个子数组分别排序;
• 合并：将两个已排序的子数组合并。

Merge Step

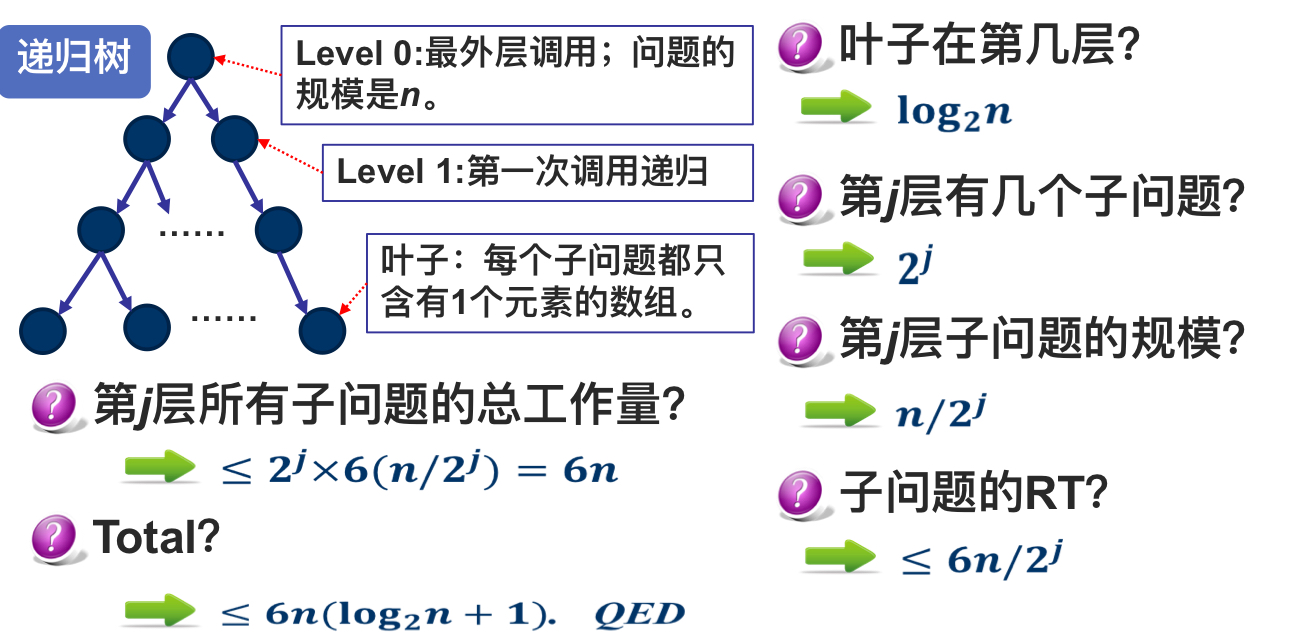
CLAIM：对于n ≥ 1的数组，MergeSort需要的运行时间T(n) ≤ $ 6n \log_2 n + 6n $

函数增长的渐进符号

Big O: 如果存在正数c和N，对于所有的n>=N，有f(n)<=c*g(n)，则f(n)=O(g(n))。

Big Omega：如果存在正数c和N，对于所有的n>=N，有f(n)>=c*g(n)，则f(n)=Omega(g(n))。

Big Theta：f(n)=Theta(g(n))，当且仅当f(n)=O(g(n))且f(n)=Omega(g(n))。

基于比较的排序

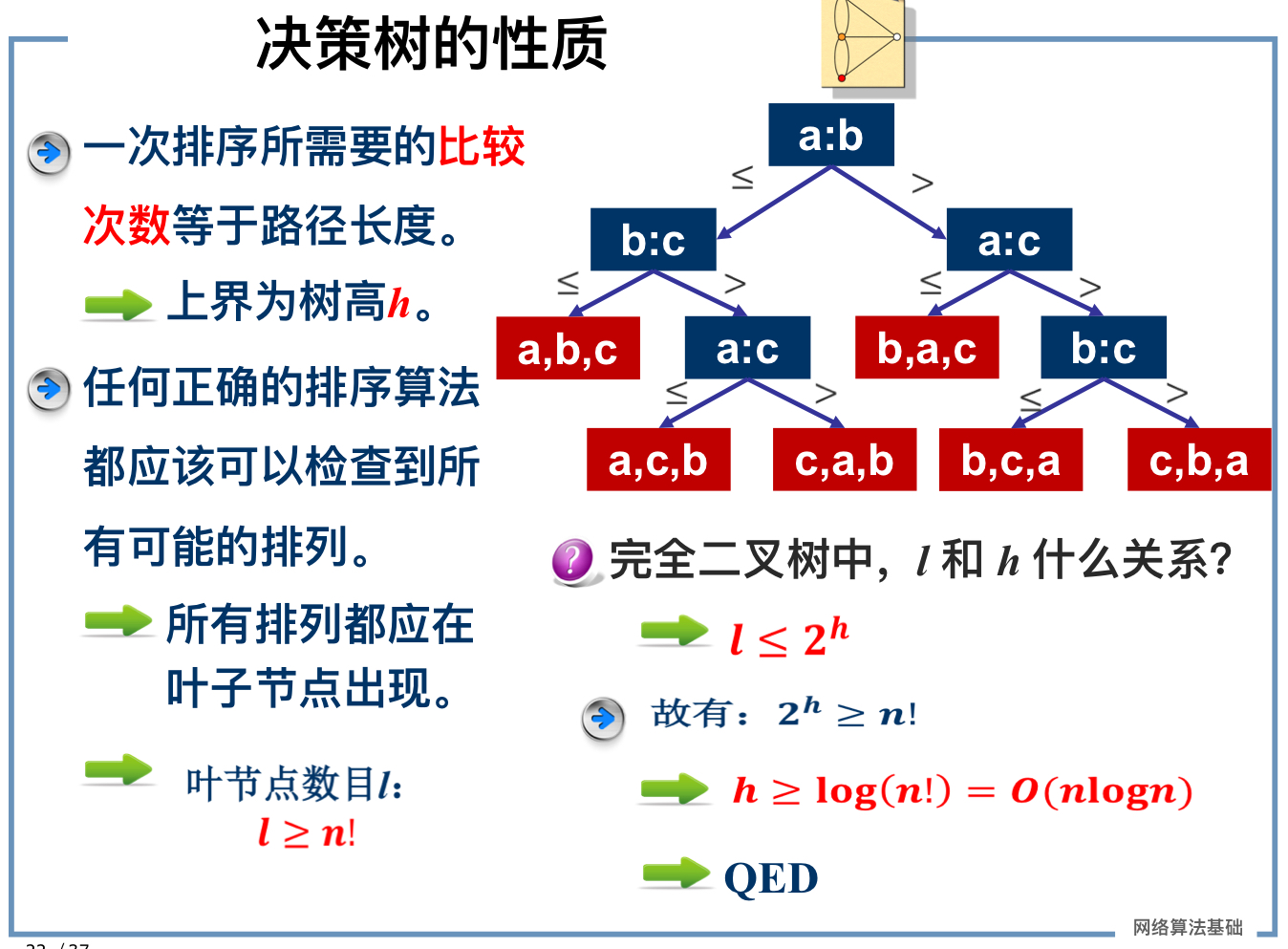
CLAIM：任何基于比较的排序算法，RT不可能低于O(nlogn)。

任何基于两两比较的排序算法都可以表达为一棵决策树（完全二叉树）。

完全二叉树：完全二叉树从根结点到倒数第二层满足完美二叉树，最后一层可以不完全填充，其叶子结点都靠左对齐。

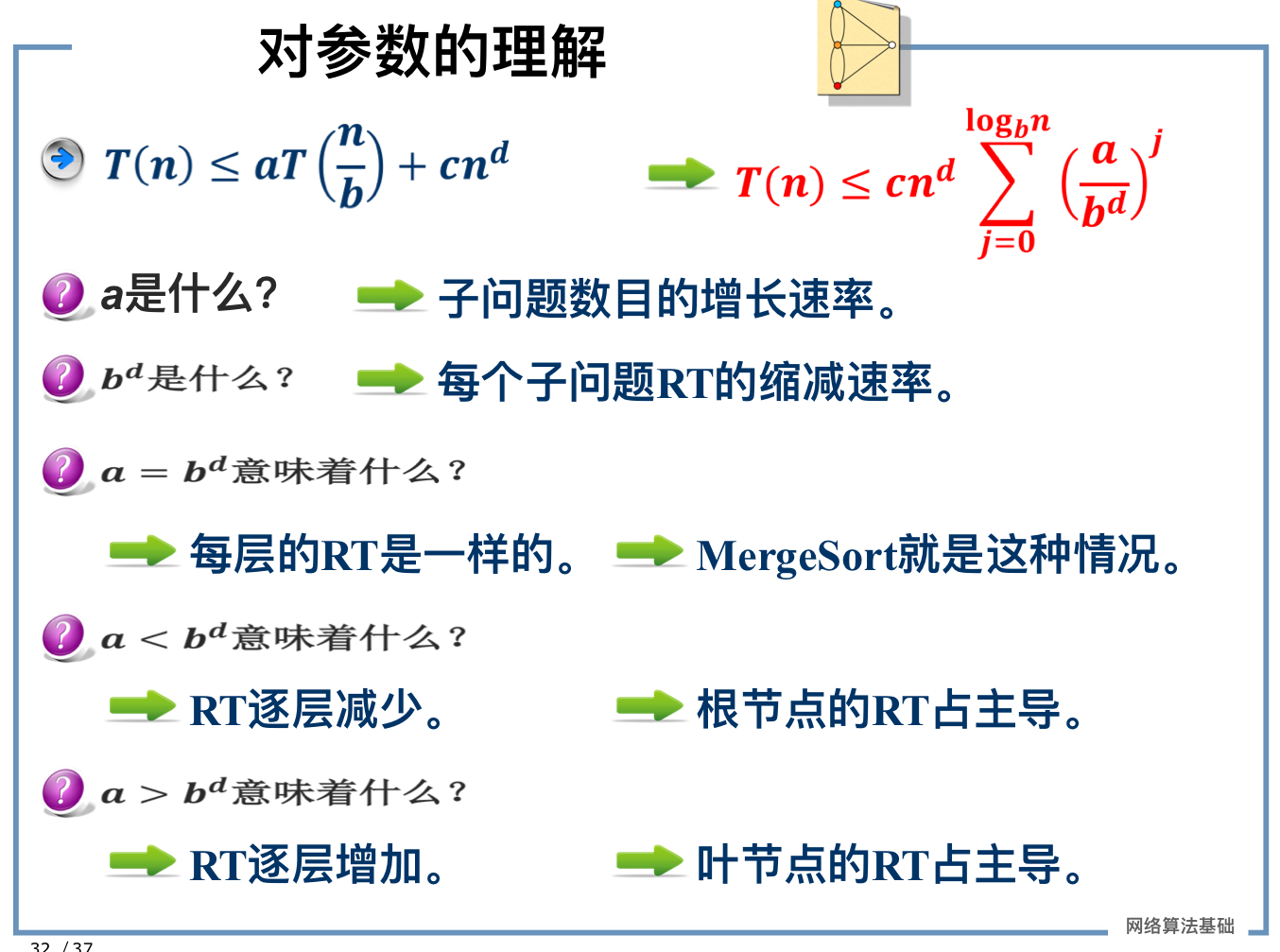
主办法（Master Method）

主定理

图简介

树

树：不包含任何圈的连通图。

生成树(Spanning Tree)：如果图G的一个子图包含了G的全部顶点，且为树，则称之为G的生成树。

图搜索

循环不变式

• 概念：每次循环开始时都要保持的性质 / 状态。
• INVARIANT：已探索集合和未探索集合应该处于正确的状态。边界点集合应准备好了。
  • 循环开始时，从边界点集合中选择一个顶点进行探索。
  • 循环结束前，将新扩展的边界点纳入集合。
• 维护边界点集合：
  • BFS：队列(FIFO)
  • DFS：堆栈(LIFO)

BFS

BFS的伪代码：

BFS(Graph, start):
B.EnQueue(s)
WHILE B is not empty:
    d=B.DeQueue();
    标记d为“已探索”
    FOR each neighbor t of d:
        IF t is not in visited:
            B.EnQueue(t)
        ENDIF
    ENDFOR
ENDWHILE

聚合分析复杂度：O(n+m)

DFS

DFS的伪代码：

DFS(Graph, start):
B.Push(s)
WHILE B is not empty:
 d = B.Pop()
 标记 d 为“已探索”
 FOR each neighbor t of d:
  IF t is not in visited:
   B.Push(t)
  ENDIF
 ENDFOR
ENDWHILE

聚合分析复杂度：O(n+m)

图的连通性

无向图的连通分量

下述等价关系的等价类：当且仅当图中具有u-v路径时，称u~v。

BFS求无向连通分量

BFS求无向连通分量的伪代码：

Loop-BFS(G):
FOR i=1 to n
	IF t is not in visited:
		BFS(G,i);
ENDFOR

聚合分析复杂度：O(n+m)

有向图的强连通分量（Strongly Connected Component,SCC）

下述等价关系的等价类：当且仅当有向图G中具有u -> v路径且具有v -> u路径时，称称u~v。

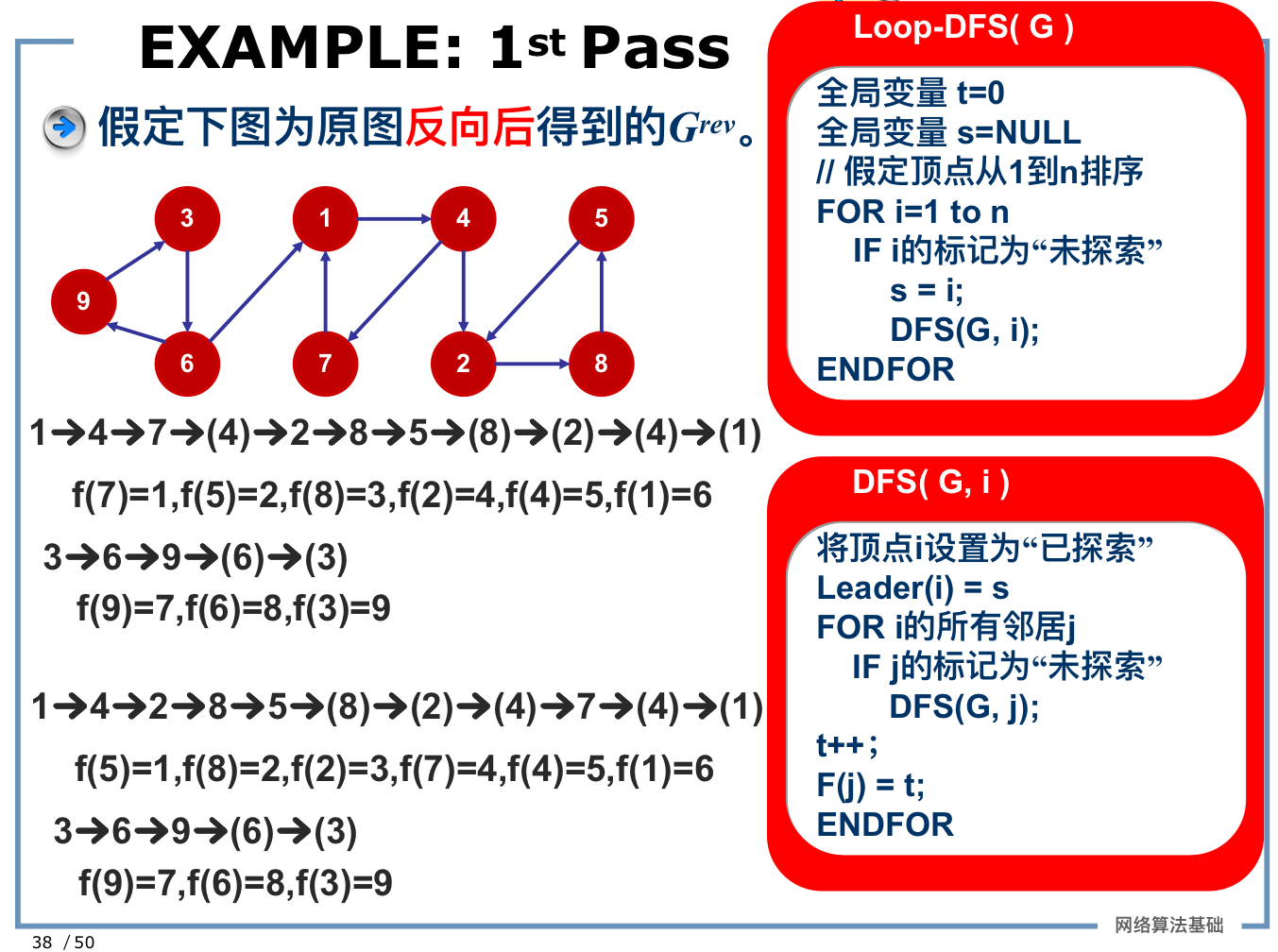
TWO-PASS算法(Kosaraju算法)

1. 构建逆图。
2. 在逆图中进行 Loop-DFS，记录每个节点的完成时间 f(v)。
3. 在原图中运行 Loop-DFS，按照逆图 DFS 完成的节点顺序进行，确定每个节点的 Leader。

聚合分析复杂度：O(n+m)

关键引理

Key Lemma：考虑有向图G中的两个临接SCC，f(v)表示顶点v在反向图G’中Loop-DFS的完成时间，则有：
$$
\max_{v \in C_1} f(v) < \max_{v \in C_2} f(v)
$$
推论：最大的f值必然在”sink“SCC中。

贪心MST

贪心vs分治

• 决策过程：
  • 分治：每个子问题的解都会考虑整个子问题的情况，逐步拆解，最终合并。
  • 贪心：每一步决策只关注当前的局部最优解，不回头。
• 全局与局部：
  • 分治：每个子问题的解可能涉及整个问题的全局结构。
  • 贪心：每一步只考虑局部最优解，期望通过局部最优解得到全局最优解。
• 解决问题的方式：
  • 分治：递归地分解问题，直到子问题足够简单直接求解。
  • 贪心：通过逐步选择当前最优的解来构建最终解。
• 是否需要回溯：
  • 分治：通常会回溯并合并结果。
  • 贪心：不会回溯，一旦做出选择就不再修改。

MST（前提：无向图）

定义：最小权重生成树T。

• 必须是无向图;
• 生成树的权重定义为树上边权重之和;
• 生成树定义为E的子集：
  1. 必须覆盖V;
  2. 无环;
  3. 连通。

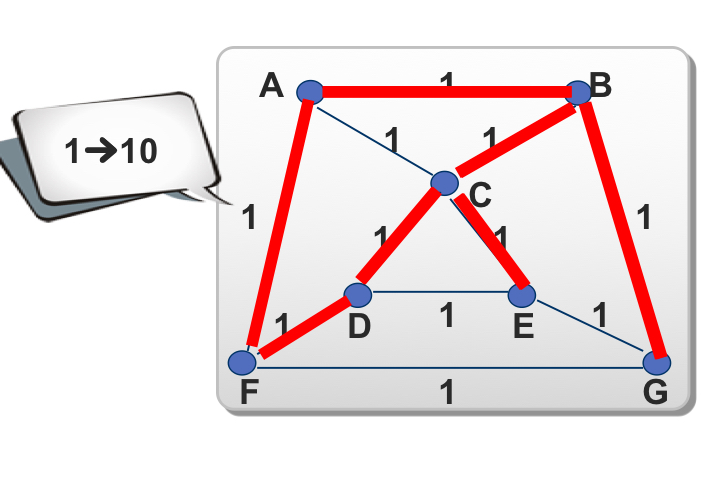
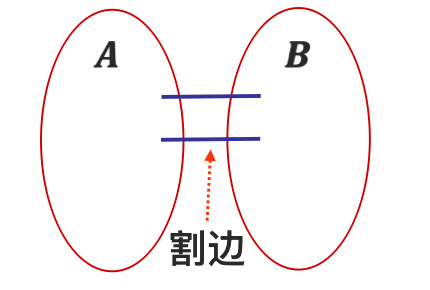
割

割的概念：图G(V，E)的一个割(Cut)是V的一个划分，该划分将集合V分为两个非空的集合。

• n个顶点的图最多有 $ 2^n-2 $ 个不同的割。

Empty-Cut引理：图G不连通，当且仅当Cut(A，B)没有割边。

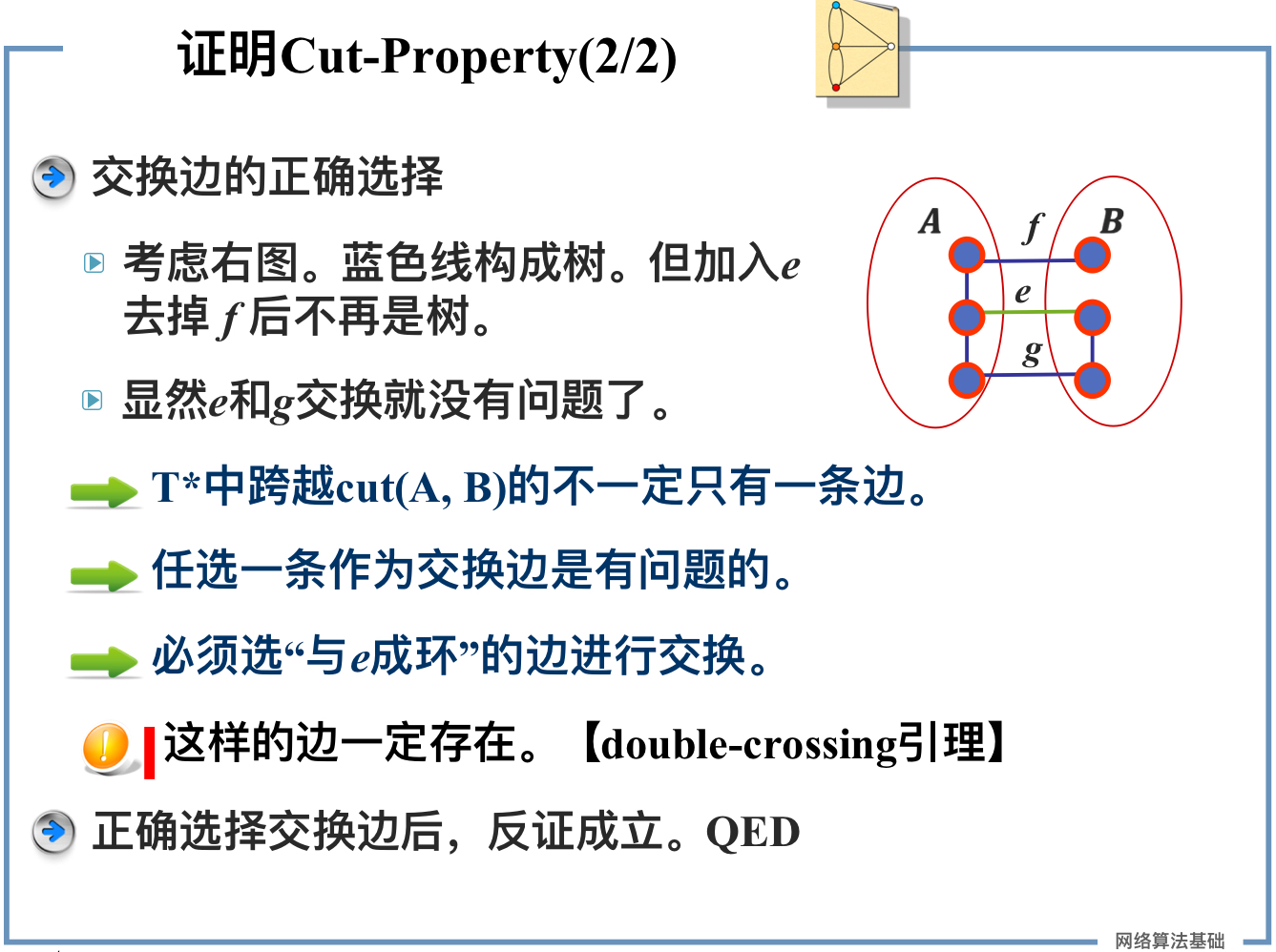
Double-Crossing Lemma：如果某个圈C⊆E中有边跨越了Cut(A，B)，则C中至少还有一条边跨越Cut(A，B)。

Lonely-Cut Corollary：如果边e是跨越了Cut(A，B)的唯一一条边，则e不可能在任一圈中。

The Cut Property：考虑图G中的一条边e，如果存在Cut(A，B)，使得e是所有跨越该割的所有边中权最小者，则e一定在G的MST中。

割的证明：

堆（Heap）

一个容器，其中元素具有key。

常规操作及对应的RT：

• Heapify：建堆 O(n)
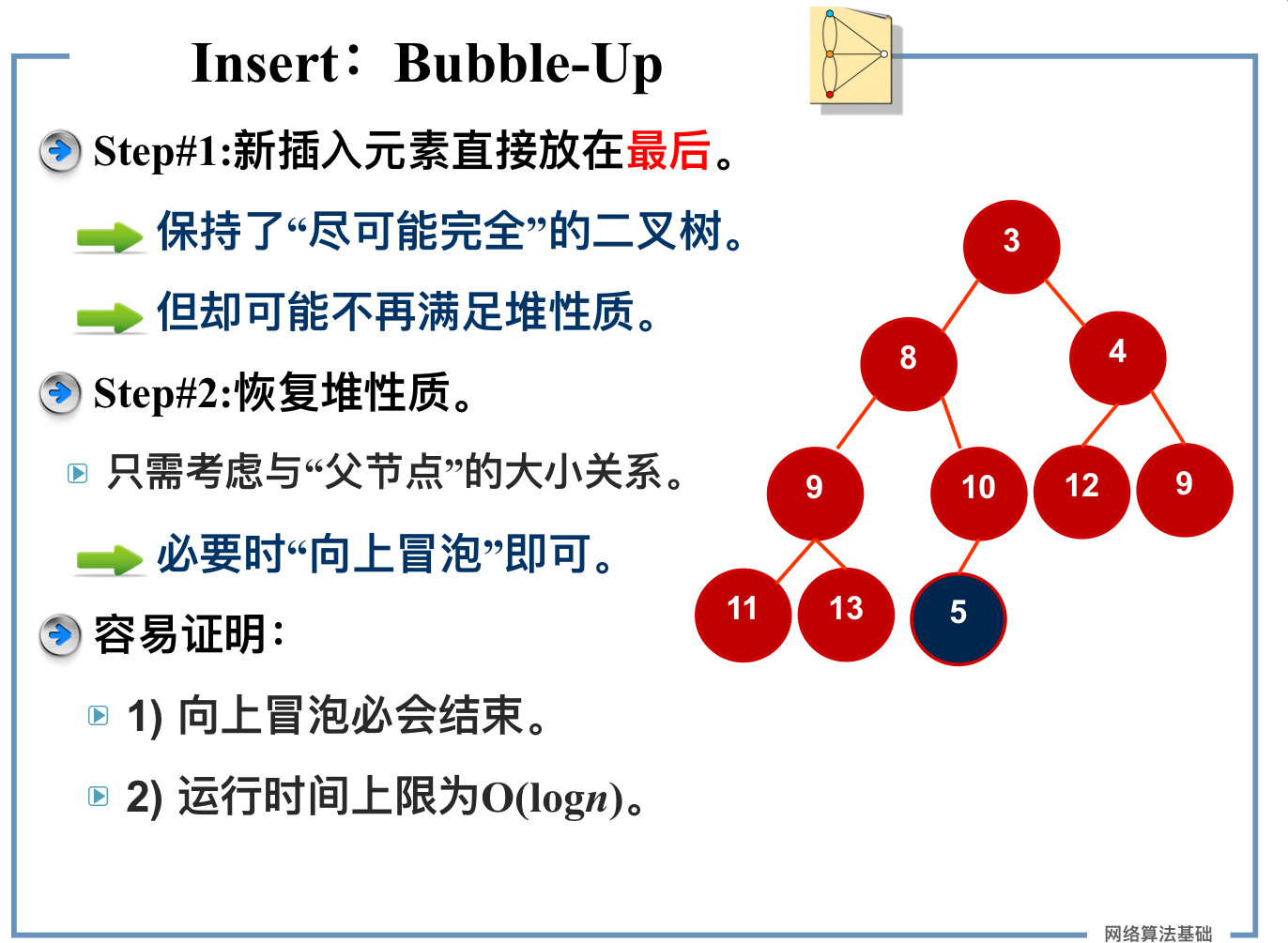
• Insert：加入一个新的对象 O(logn)
• Extract-Min：从堆中取出具有最小key的元素 O(logn)
• Delete：删除指定元素 O(logn)

Heap Property

• 堆是一颗有根，二叉，尽可能完全的树。
• 任何节点的key都不大于其所有子代的key。 ——> 根元素具有最小key

用数组实现堆

• Parent (i) = i / 2 （下标i为奇数时向下取整）
• LeftC (i) = 2i
• RightC (i) = 2i + 1

Prime算法

基本思想：

• 从一个节点开始（任意选择一个节点作为起点），将它加入生成树。
• 找到当前生成树中所有节点与其他节点之间的边，选择权重最小的边。
• 将与该边相连的节点加入生成树，更新最小边的权重，重复选择最小边的过程。
• 直到所有节点都被加入到生成树中。

Pim的伪代码：

Prim(Graph, start):
    初始化最小生成树的边集合 MST = {}
    初始化一个优先队列 Q，用于存储每个节点及其最小边的权重
    对于每个节点 v ∈ Graph:
        设置 v 的最小权重为无穷大（∞）
    设置 start 节点的最小权重为 0，并将其加入 Q

    WHILE Q is not empty:
        选择 Q 中最小的权重的节点 u
        标记 u 为“已加入到最小生成树”

        对于 u 的每个邻居 v:
            IF v is not in MST AND weight(u, v) < v 的当前权重:
                更新 v 的最小权重为 weight(u, v)
                将 v 更新到 Q 中，以反映其新的最小权重

        ENDFOR
    ENDWHILE

Prim算法的证明：

用堆实现Prim：

Prim(Graph, start):
    初始化最小生成树 MST = {}
    初始化最小堆 MinHeap
    初始化一个集合 Visited，用于记录已加入 MST 的节点
    将 (0, start) 插入 MinHeap  // (边的权重, 节点)
    初始化 total_weight = 0  // 记录最小生成树的总权重	
	WHILE MinHeap is not empty:
    	(weight, node) = MinHeap.Pop()  // 取出当前权重最小的边
   	 IF node 已在 Visited:
    	    CONTINUE  // 如果该节点已经在 MST 中，跳过

  	  标记 node 为已访问
  	  total_weight += weight  // 累加权重
  	  MST.Add(node)

	    FOR each (neighbor, edge_weight) in Graph[node]:  // 遍历邻居
     	   IF neighbor 不在 Visited:
       	     MinHeap.Push((edge_weight, neighbor))  // 只加入未访问的节点

	RETURN MST, total_weight

复杂度分析：

• n次Extract-Min：O(nlogn)
• m次Delete和m次Insert：O(mlogn)

总RT = O(nlogn)+O(mlogn) = O(mlogn)

Kruskal算法

基本思想：

• 按权重升序对边排序。
• 按序逐条检查边。
• 只要不成环，就将边加入T。

Kruskal的伪代码：

Kruskal(Graph):
    初始化最小生成树 MST = {}
    初始化并查集（Union-Find）来管理连通性
    按照权重从小到大排序 Graph 的所有边 EdgeList
	FOR (u, v, weight) in EdgeList:  // 遍历排序后的边
   	 IF u 和 v 不在同一个连通分量 (Find(u) ≠ Find(v)):
    	    MST.Add((u, v, weight))  // 加入最小生成树
  	      Union(u, v)  // 合并连通分量
  	  IF MST 的边数 == V - 1:
     	   BREAK  // 最小生成树构建完成
	RETURN MST

Kruskal算法的证明：

UNION-FIND算法

Union-Find（并查集）是一种高效的数据结构，主要用于处理动态连通性问题。它支持两种核心操作：

1. Find(x)：查找元素 x 所属的集合（返回它的代表元素）。
2. Union(x, y)：合并 x 和 y 所在的两个集合。

核心思想：

• 每个集合用一棵树表示，树的根节点作为该集合的代表元（代表元素）。
• Find(x) 操作用于查找 x 所在集合的代表元（根节点）。
• Union(x, y) 操作用于合并两个集合，将其中一个集合的根节点指向另一个集合的根。

Dijkstra算法

Dijkstra的前提：无负权图（源点到第一层点的权重可为负值），避免负圈。

Dijkstra的基本思路：

1. 初始化：

• 设 dist[s] = 0（起点到自身的距离为 0），其他所有点 dist[v] = ∞（起始时认为未知）。
• 用一个**优先队列（最小堆）**维护当前已发现的最短距离点。

2. 贪心扩展：

• 每次从未访问的节点中选取当前 dist[v] 最小的点 u。
• 遍历 u的所有邻居 v，尝试松弛：
  • 如果 dist[u] + w(u, v) < dist[v]，更新 dist[v]，并将 v 加入优先队列。

3. 终止：所有节点均已访问，或优先队列为空（所有可达点已确定最短路径）。

Dijkstra的伪代码：

Dijkstra(Graph, start):
    初始化 dist[]，所有点设为 ∞，dist[start] = 0
    初始化优先队列 PQ，插入 (0, start)  // (当前最短距离, 顶点)
    初始化 visited[] 记录已确定最短路径的点

    WHILE PQ 不为空:
        (d, u) = PQ.Pop()  // 取出当前最短距离的点
        IF u 已访问:
            CONTINUE
        标记 u 为已访问

        FOR each 邻居 (v, weight) of u:
            IF dist[u] + weight < dist[v]:  // 进行松弛操作
                dist[v] = dist[u] + weight
                PQ.Push((dist[v], v))  // 将 v 加入优先队列
    
    RETURN dist[]

循环桶

桶（Bucket） 是一种数据存储和分类的方法，可以根据某种规则（如哈希值、时间、范围等）将数据映射到不同的桶中，以加快查询、存储或计算的效率。

循环桶将数据按照一定规则分配到有限个桶（Bucket）中，并循环使用这些桶。

循环桶的核心特点

1. 固定数量的桶（N 个）：
   • 设定 N 个桶，编号从 0 到 N-1，它们按照顺序排列成一个循环结构。
   • 访问时基于取模（modulo）运算，保证访问永远落在 0 ~ N-1 之间。
2. 循环访问（Modulo 取模）：
   • 计算索引 index = (当前时间 t) % N，从而使得时间到了 N 之后会回到 0，形成循环管理。

用循环桶实现Dijkstra算法：

CLAIM：Dijkstra算法中最多只需要C+1个桶。

• 永久标记的顶点和非边界顶点不在桶中。
• 边界点的距离标记不会超过A[i]+C（i为当前标记点）
• 顶点x的桶的编号：A[x]mod(C+1)

Dijkstra_CircularBucket(Graph, start):
    初始化 dist[]，所有点设为 ∞，dist[start] = 0
    初始化桶 Bucket[]，桶的数量为 C+1，存储每个距离区间的节点
    初始化 visited[]，记录顶点是否已被永久标记
    
    将起点 start 放入 Bucket[0] 中（dist[start] = 0）
    
    WHILE 有节点未被永久标记:
        从桶中找出具有最小距离的非永久标记的边界点 u
        标记 u 为永久标记，并从桶中移除 u
        
        FOR 每个邻居 v of u:
            IF v 没有被永久标记:
                IF dist[u] + w(u, v) < dist[v]:
                    dist[v] = dist[u] + w(u, v)  // 松弛操作
                    将 v 放入 Bucket[dist[v] mod (C + 1)] 中  // 根据 dist[v] 放入桶
                    更新 v 的距离标记

    RETURN dist[]

复杂度分析：O(m+nC)

Dijsktra算法扩展

单源单宿最短路问题

问题描述：给定图G，给定顶点s和d，求从s到d的最小权重路径。

解决方式：增加一个判断分支，d被永久标记时终止循环。

1111111111111111

文章目录