OverView

前端:路径寻找

基于搜索

图搜索基础
Dijkstra and A*
Jump Point Search

基于采样

Probabilstic Road Map
RRT
RRT* / Informed RRT

基于运动学动态路径寻找

State-state Boundary Value Optimal Control Problem
State Lattic Search
Kinodynamic RRT*
Hybrid A*

后端:轨迹生成

MINIMUN SNAP TRAJECTORY GENERATION

SOFT AND HARD CONSTRAINED TRAJECTORY OPTIMIZATION

MAP

Occupancy grid map

github:https://github.com/ANYbotics/grid_map

排列紧密
结构化
索引队列访问

缺点:当切分过于细密时空间占用率大.

Octo-map

github:https://github.com/OctoMap/octomap_mapping

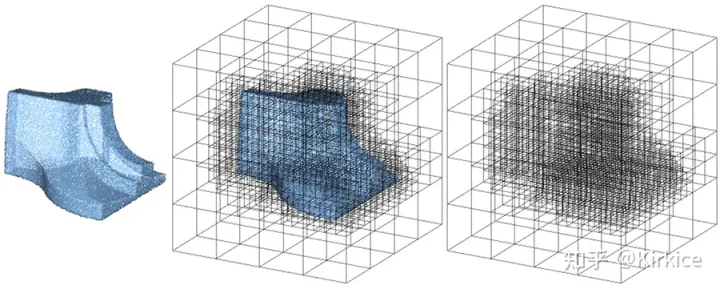
地图中大部分为稀疏部分,使用八叉树的数据结构储存.如果一个区块没有障碍物,不再细分该区块;如果一个区块有障碍物则细分至最小包含该障碍物的区块.

Octree

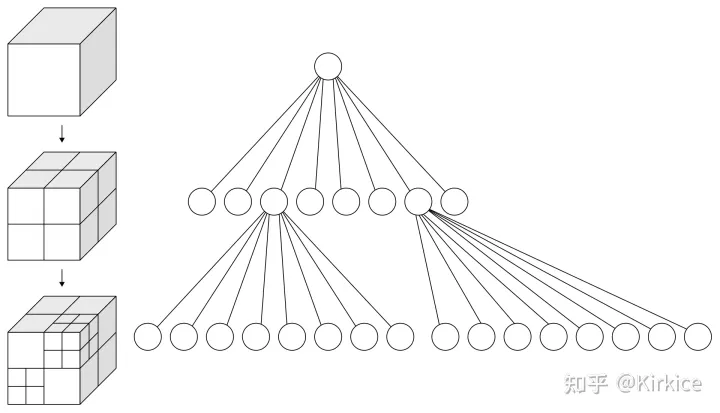
八叉树（Octree）是一种用于描述三维空间的树状数据结构。八叉树的每个节点表示一个正方体的体积元素，每个节点有八个子节点，将八个子节点所表示的体积元素加在一起就等于父节点的体积。八叉树是四叉树在三维空间上的扩展，二维上我们有四个象限，而三维上，我们有8个卦限。八叉树主要用于空间划分和最近邻搜索。

实现Octree的原理:

将当前的立方体细分为八个子立方体。
如果任何一个子立方体内包含多个点，则将其进一步细分为八个子立方体。
重复以上操作使得每个子立方体内包含最多一个点。

八叉树1

八叉树2

排列稀疏
结构化
非直接索引访问(树的查询)

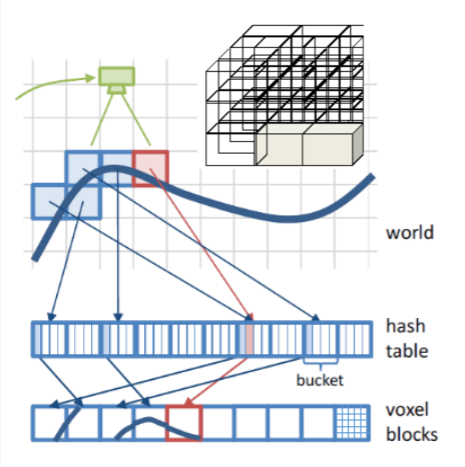
Voxel hashing

github:https://github.com/niessner/VoxelHashing

记录存在碰撞的区块 —-> 哈希表,字典

一个bucket中划分为更小的voxel blocks

Voxel

排列最稀疏
结构化
非直接索引访问(字典查询)

Point Cloud Map

无序
无法通过索引队列访问(除非自发遍历)

TSDF map

Truncated Signed Distance Functions (截断/有符号/距离函数)

github:

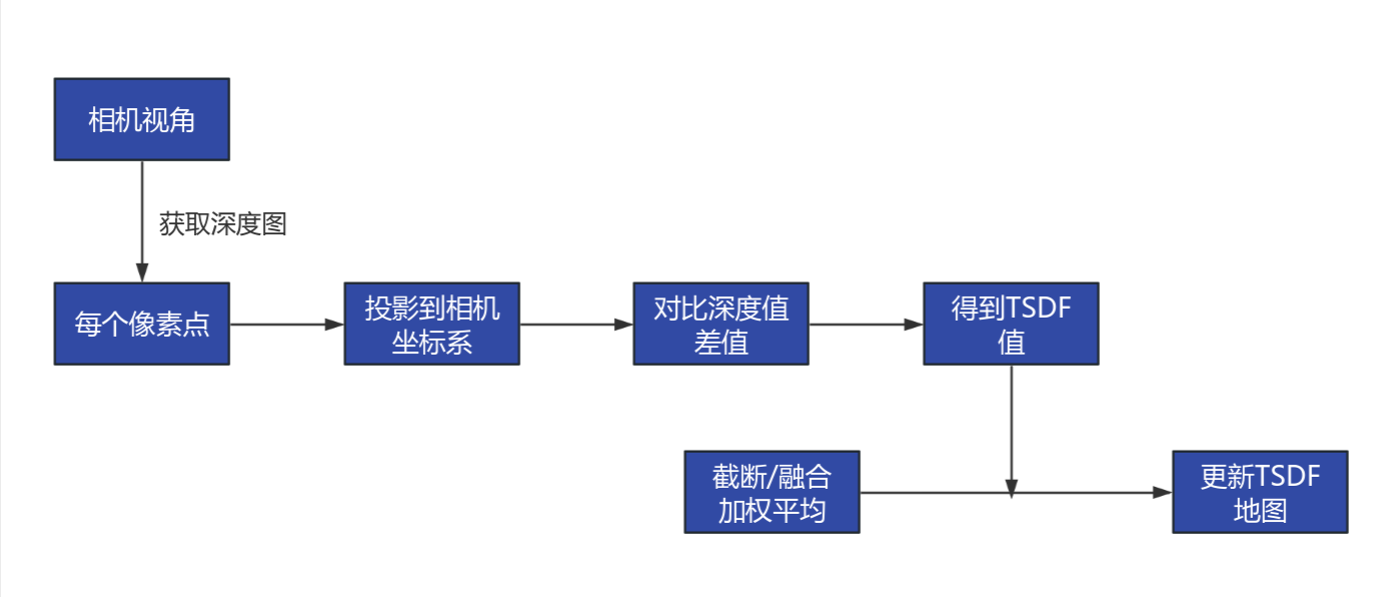
TSDF 是一种用于表示3D空间表面的体素网格地图.

Signed Distance Function (SDF)

对于空间中任意一点 x，SDF 给出它到最近表面的距离 d：
$$
SDF(x)=±d
$$

+d：点在表面外部（通常指相机方向）
−d：点在表面内部
d=0：点在表面上（即零交叉点）

Truncated SDF（TSDF）

真实计算中远离表面部分的距离信息不重要且不准确，因此会进行截断：

若 ∣d∣> μ，则 TSDF 值为截断值。
μ 是截断距离阈值（truncation distance）。

Voxel Grid（体素网格）

TSDF 存在于一个 3D 网格中（类似立方体像素）：

每个体素（voxel）存储：
- 当前体素的 TSDF 值
- 加权平均值（来自多个观测帧）
- 权重（用于融合多个观测）

TSDF1

TSDF2

ESDF Map

Euclidean Signed Distance Field 欧几里得有符号距离场

以 3D 网格（体素）的形式表示环境中每一点到障碍物最近点的欧几里得距离，并附带符号来表示点位于障碍物内部或外部。局部ESDF地图:只记忆感兴趣部分的ESDF值.

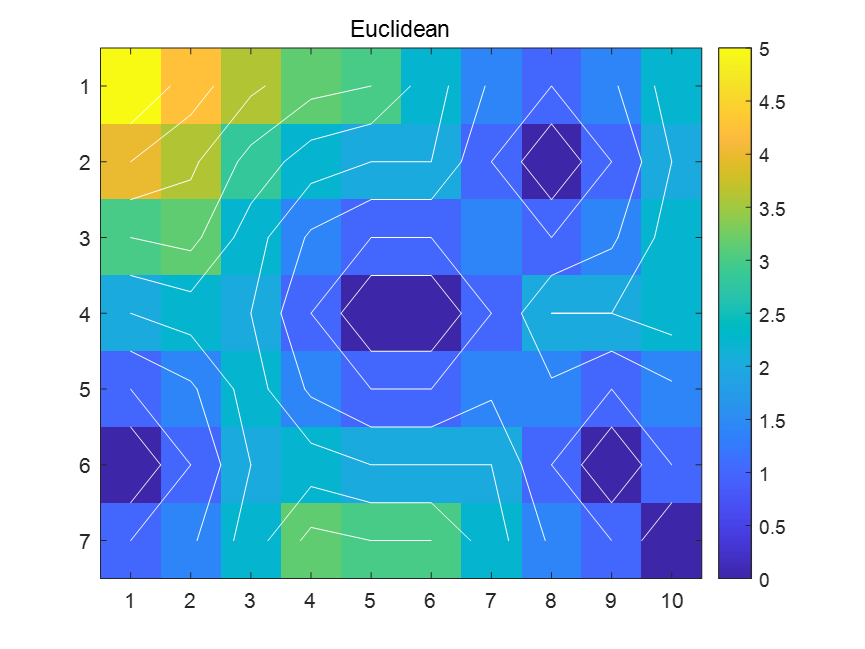
ESDF1

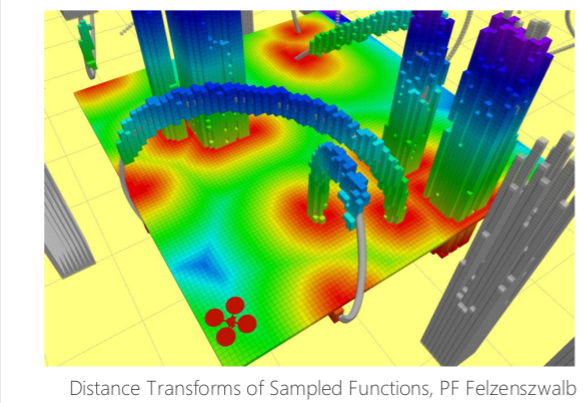
ESDF2

Free-space Roadmap

概率路线图 —-> 安全通行区域,使用凸多边体表示

得到的是一个宽阔的解空间

Voronoi Diagram Map

高效利用ESDF提取地图骨架 —-> 稀疏

基于搜索的路径寻找

A*

A*算法在Dijkstra算法的基础上引入了启发函数(贪心思想)，启发函数是对当前节点到目标节点所需代价的预估.启发式函数一般使用曼哈顿距离、欧几里德距离。

从起点开始，将其加入待探索的节点集合（open set）。

每次选择 f 值最小的节点进行扩展，其中 f(n) = g(n) + h(n)

g(n) 是从起点到当前节点的实际代价

h(n) 是从当前节点到终点的启发式估计（如直线距离）

对当前节点的所有相邻节点，计算新的 g 值，更新路径记录。

如果发现更优路径（g 值更小），则更新该邻居的记录，并加入 open set。

重复以上步骤，直到终点被选中扩展，表示找到最短路径。

通过路径记录表回溯，重建从起点到终点的完整路径。

伪代码

• 维护一个优先级队列来存储所有待扩容节点
• 所有节点的启发式函数h(n)是预定义的
• 优先级队列初始化为起始状态 X S
• 对图中所有其他节点赋值g(X S) = 0, g(n) = infinite
• Loop
    •如果队列为空，则返回FALSE；BREAK;
    •从优先级队列中删除f(n)=g(n)+h(n)最小的节点“n”
    •将节点“n”标记为展开
    •如果节点“n”是目标状态，返回TRUE；BREAK;
    •对于节点n的所有未展开的邻居 m
		•If g(m) = infinite
			• g(m)= g(n) + Cnm
    •对于节点n的所有未展开的邻居 m
		•If g(m) = infinite
			• g(m)= g(n) + Cnm
			• Push node “m” into the queue
		•If g(m) > g(n) + C nm
			•g(m)= g(n) + Cnm
	•end
• End Loop

Weighted A* Search

Sub-Optimal Solution

通过人为加大启发函数的影响力来获得更快的搜索速度，以牺牲路径最优性为代价。

f = g + εh, ε > 1 =bias towards states that are closer to goal.

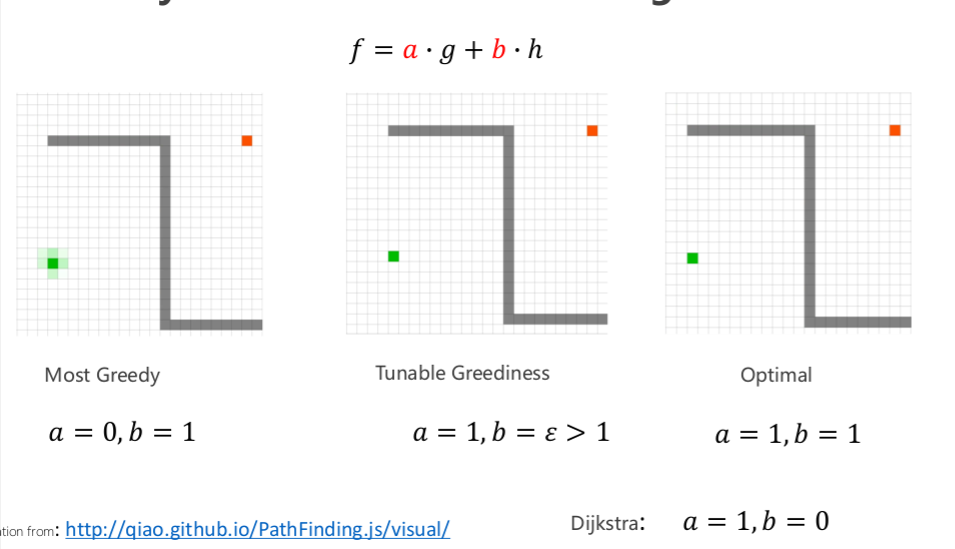
Weighted_A*_Search

Most Greedy（最贪婪）
参数：a=0,b=1
只考虑启发式代价，完全不考虑当前路径代价
结果：趋向于直接朝目标点移动，但路径不一定最短或最优

Tunable Greediness（可调贪婪度）
参数：a=1,b=ε>1
综合考虑当前路径和启发式估计，但偏向启发式
结果：平衡探索性和效率，路径更合理

Optimal（最优路径）
参数：a=1,b=1
平等考虑已知路径和启发估计
结果：找到最优路径

Dijkstra算法
参数：a=1,b=0
完全不使用启发式，只靠实际代价 g,效率低

A*的实施流程

建立地图 → 生成网格节点数组
设定障碍 → 标记不可达节点
编写邻居搜索函数
编写A*主循环：
- 从openList中取出f值最小的节点
- 计算邻居的g/h/f值，加入openList
- 更新已访问节点（closedList）
使用priority_queue或multimap优化性能

最好的启发函数

最好:tight,正确的最短距离函数

二维最佳启发函数:
$$
h2D=(dx+dy)+(2
−2)⋅min(dx,dy)
$$
三维最佳启发函数:

我们记 dx,dy,dz为三维网格中当前点与目标点在三个轴上的距离（均为非负整数），有：
$$
h3D=dmin⋅3+(dmid−dmin)⋅2+(dmax−dmid)⋅1
$$
其中：dmin,dmid,dmax是 dx,dy,dzdx,dy,dz 的排序结果，使得

$$
dmin≤dmid≤dmax
$$

Tie Breaker

平局处理器,打破 f 值相等时的探索顺序

问题:

A* 会选取 f 值最小的节点扩展（f=g+h）

但在一些情形下，很多节点的 f 值完全相等,尤其是在网格图中启发函数不够 tight 的时候

导致算法要探索很多不必要的节点，降低效率

解决方法:

人为干扰 h，让 f 值不同:

将原来的启发函数 h乘上一个微小因子：
$$
h=h×(1.0+p)
$$
其中：
$$
p < \frac{\text{最小步长代价}}{\text{预期路径总长度}}
$$
这样能 轻微打破平局，减少无效扩展

代价是轻微地破坏启发式的“可采纳性”（admissibility），但常常实际无影响或带来更好效率.

优先选 h值小的节点

如果两个节点 f 一样，选择 h 小的那个（靠近终点）

加入伪随机干扰项（Deterministic random）

给每个节点加一个唯一扰动，保持一致性但不完全对称

优先靠近起点-终点连线的路径

$$
cross=∣dx1×dy2−dx2×dy1∣
$$

这其实是在衡量点偏离直线的“面积”，越小越靠近理想路径。

Jump Point Search

核心思想:在两点之间没有障碍物时，中间的节点不考虑,只考虑重要节点.

邻居修剪 Neighbor Pruning

灰色节点：较差的邻居，当去到它们时，没有分值的路径更便宜。丢弃。
白色节点：自然邻居。

只需要考虑自然邻居.

Neighbor Pruning

强迫邻居 Forced Neighbors

节点X的邻居节点有障碍物，且X的父节点P经过X到达N的距离代价，比不经过X到大N的任一路径的距离代价都小，则称N是X的强迫邻居。

有相邻的障碍
红色节点是强制邻居。
一条从父母到他们通过障碍的更便宜的路径被阻断。

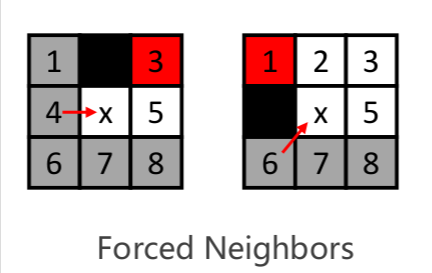
Forced Neighbors

跳点(Jump Point)：什么样的节点可以作为跳点
(1)节点 A 是起点、终点.
(2)节点A 至少有一个强迫邻居.
(3)父节点在斜方向(斜向搜索)，节点A的水平或者垂直方向上有满足 (1)、(2) 的节点

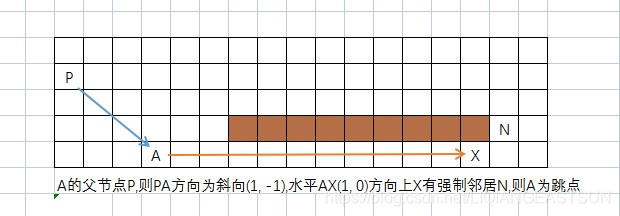
Jump Point

跳点搜索中，会递归地检查路径上的邻居节点是否是“跳点”。在检查对角线方向前，会优先尝试直线方向。只要某个节点通往某些邻居的最短路径必须经过它，它就会被标记为跳点。同时，对“强制邻居”不能剪枝，必须展开。

基于采样的路径寻找

Probabilistic Road Map

图结构

将规划分为两个阶段：
·学习阶段
·查询阶段

检查采样配置和连接的样本之间的碰撞可以有效率地完成任务。
数量相对较少的里程碑和局部路径足以捕获的连通性。

限制路径点连接的长度避免图结构过于复杂

学习阶段:

在c空间中采样N个点
删除碰撞点

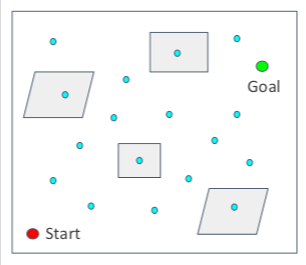
PRM-Learning1

连接到最近的点，并获得无碰撞段。
删除碰撞段

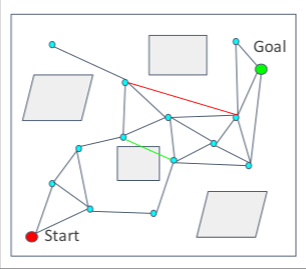
PRM-Learning2

查询阶段:

在路线图上搜索，找到从起点到终点的路径目标（使用Dijkstra算法或A*算法）。
路线图现在类似于网格地图

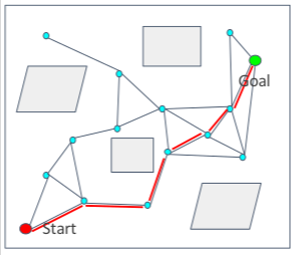
PRM-Query

优点

概率完备

缺点

要求解决两点边值问题
在状态空间上构建图，但不特别关注生成路径
效率不高

Lazy collision-checking

效率低: PRM（Probabilistic Roadmap）或 RRT（Rapidly-exploring Random Tree) 需要频繁地检查从一个配置到另一个配置（或状态）之间的路径是否与障碍物发生碰撞。但碰撞检测是一个昂贵的计算操作，尤其在高维空间或复杂环境中，频繁的碰撞检测会成为性能瓶颈。

不考虑采样点和生成分段碰撞（懒惰）

先构建图（PRM）或树（RRT）时不立即检查碰撞，等到真正要使用这条路径时（例如在查询最短路径、或者将路径从树/图中提取出来时），再执行碰撞检测。

PRM+Lazy collision-checking

构建 roadmap：采样节点、连接边，不做碰撞检测。
查询路径：使用 A* 或 Dijkstra 等算法找到一条从起点到终点的路径。
在该路径上进行逐段碰撞检测：
- 如果全部无碰撞，路径有效；
- 如果某段有碰撞，将该边标记为无效（不可达），从图中删除，重新搜索。

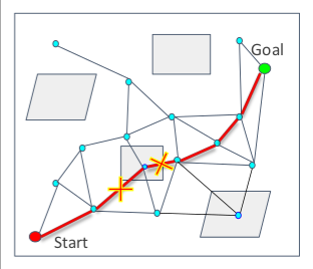
Lazy collision-checking

Rapidly-exploring Random Tree

核心思想:

通过生成next构建树状态在树中通过执行随机控制,从起点开始，不断向随机方向扩展一棵树，迅速探索整个状态空间。

伪代码:

RRT伪代码

初始化一棵树 T，将起始点 X_init 作为树的根节点。
循环:
在整个状态空间中随机采样一个点 X_rand，用于探索新方向。
找出树 T 中距离 X_rand 最近的已有节点 X_nearest。
从 X_nearest 朝 q_rand 方向延伸一个固定步长delta，生成新点 X_new。

如果新点 X_new 是可行的（比如不与障碍物碰撞），则执行以下操作:

把这个新点 X_new 加入树中，作为新的节点。
在树中添加一条从 X_nearest 到 X_new 的路径边。
返回整个搜索生成的树 T，它包含从起点开始探索出来的路径结构。

**提前停止的条件：**因为每一段树枝的末端都是Xnew，所以每产生一次Xnew节点，我们都判断一下Xnew与终点之间的距离，看这个距离是否小于步长，如果小于步长且没有经过障碍物，则就直接把Xnew与终点进行相连。

优点:
·旨在找到从起点到目标的路径
·比PRM更有针对性
缺点:
·非最优解
·效率不高,在 narrow环境 中效率低
·整个空间取样

KD树

Kd-Tree，即K-dimensional tree，是一棵二叉树，树中存储的是一些K维数据。在一个K维数据集合上构建一棵Kd-Tree代表了对该K维数据集合构成的K维空间的一个划分，即树中的每个结点就对应了一个K维的超矩形区域（Hyperrectangle）。

关键术语:

维度（K）：表示数据点所在的空间维数。例如，二维空间中的点有x和y坐标，三维空间中的点有x、y、z坐标。
节点：KD树的每个节点包含一个K维点及其分割超平面的信息。
超平面：在K维空间中用于将空间划分为两个部分的（K-1）维子空间。例如，二维空间中的超平面是直线，三维空间中的超平面是平面。

构建步骤:

输入数据：假设有N个K维数据点。
选择分割维度：按照循环顺序选择当前维度。例如，第一个维度（x轴）用于根节点，第二个维度（y轴）用于其子节点，依此类推。
选择分割值：在当前分割维度上找到中位数点，将其作为当前节点。
划分数据：
- 左子集：所有在当前分割维度上小于中位数点的点。
- 右子集：所有在当前分割维度上大于中位数点的点。
递归构建子树：对左子集和右子集重复上述步骤，直到所有点都被包含在树中。
终止条件：当某一子集为空时，递归终止。

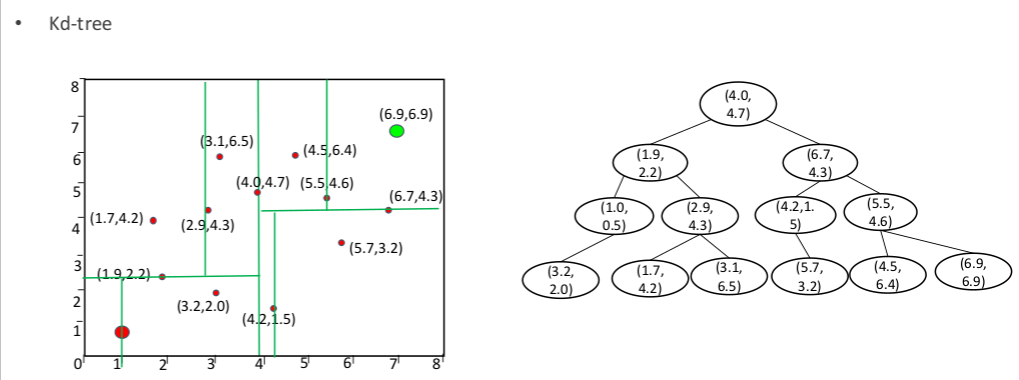
一个创建KD树的例子

使用KD树提高路径规划效率

Bidirectional RRT / RRT-Connect 双向快速扩展随机树

初始化两棵树：T_start 以 q_start 为根，T_goal 以 q_goal 为根。

重复以下过程直到路径找到或迭代上限：
a. 从状态空间中采样一个随机点 q_rand。
b. 使用 Extend 操作从 T_start 向 q_rand 延伸，得到 q_new。
c. 如果扩展成功：
i. 使用 Connect 操作让 T_goal 向 q_new 不断扩展，直到无法前进。
ii. 如果两个树在某个点连接，则路径找到。
d. 交换 T_start 和 T_goal。

项目	单向 RRT	双向 RRT（RRT-Connect）
扩展方向	只从起点扩展	起点和终点同时扩展
搜索速度	较慢	更快，更高效
成功率	容易陷入复杂障碍	双向推进更容易绕障碍
路径质量	一般	更好
复杂性	低	高

Optimal sampling-based path planning methods

在传统采样方法（如 RRT、PRM）的基础上，进一步加入了路径最优性保证的算法。最经典的代表是 RRT*

RRT*

RRT*伪代码

Choose Best Parent：在新节点周围半径内的已有节点中，选择一条“代价最小”的路径作为父节点；

Rewire：反过来看新节点是否能以更小的代价更新周围节点的父节点。

Kinodynamic-RRT*

更改Steer（）函数以适应机器人的运动或其他限制导航(曲线)

Advanced Sampling-based Methods

Inform RRT*

一旦找到一条路径，其代价为 c_best，就只在以下区域采样：

从起点 q_start 到终点 q_goal 的椭球体区域（Ellipsoidal Sampling Space）
半长轴为 c_best/2，焦点为起点与终点，构成一个最短路径所有可能穿过的区域。

Inform RRT*

Cross-entropy motion planning

初始化一个轨迹分布模型
- 比如用高斯分布建模一条轨迹（多个中间点组成）
- 初始均值：可能是直线路径，初始方差大
采样多个轨迹

每条轨迹是从当前分布中采样得到的一个完整路径（可加速度约束等）
评估轨迹代价:碰撞检测、路径长度、平滑性、目标接近度等
选取表现最好的轨迹（Top-k）:选出“精英轨迹”，即代价最小的那一部分
**用精英轨迹更新分布参数:**更新高斯均值和协方差，使下次采样更集中于好路径附近
迭代:重复 2-5，直到满足终止条件（如达到最小代价、收敛、超时等）

Path_planning_learning

OverView

前端:路径寻找

基于搜索

基于采样

基于运动学动态路径寻找

后端:轨迹生成

MINIMUN SNAP TRAJECTORY GENERATION

SOFT AND HARD CONSTRAINED TRAJECTORY OPTIMIZATION

MAP

Occupancy grid map

Octo-map

Voxel hashing

Point Cloud Map

TSDF map

Signed Distance Function (SDF)

Truncated SDF（TSDF）

Voxel Grid（体素网格）

ESDF Map

Free-space Roadmap

Voronoi Diagram Map

基于搜索的路径寻找

A*

Weighted A* Search

A*的实施流程

最好的启发函数

Tie Breaker

Jump Point Search

基于采样的路径寻找

Probabilistic Road Map

学习阶段:

查询阶段:

Lazy collision-checking

PRM+Lazy collision-checking

Rapidly-exploring Random Tree

KD树

Bidirectional RRT / RRT-Connect 双向快速扩展随机树

Optimal sampling-based path planning methods

RRT*

Kinodynamic-RRT*

Advanced Sampling-based Methods

Inform RRT*

Cross-entropy motion planning